مهندسی ساختمان شاخه ای از مهندسی است که به طور اخص در ارتباط با طراحی و تحمل بارسازه ها است. به عنوان مثال مهندسی ساختمان به صورت عمده درتکمیل و به کار گیری ماشین آلات جهت طراحی سازه ها نظیر پل ها، دیوارها (شامل دیوار حائل)، سد ها، تونل ها و غیره می باشد.
مهندسین سازه لازم است طرح
ساختمان ها رابه طریقی انجام دهند که در زمان استفاده ساختمان به خوبی عمل و انجام وظیفه نماید. آنها نباید شکسته و منهدم شوند ، نباید خم، چرخش و لرزش داشته باشند. به علاوه مهندسین ساختمان مسئول به وجود آوردن و ایجاد استفاده موثر و اقتصادی از سرمایه ها و مواد
مصالح برای رسیدن به اهداف تعیین شده برای سازه می باشند به صورت مشابه مهندسین سازه کار آموز می تواند طراحی
تیرهای سازه و
ستون ها و کفهای ساختمان های جدید را انجام دهند شامل محاسبه بار وارده برروی هر عضو و ظرفیت تحمل بار متفاوت در ساختمان
«فولاد-
چوب-
آجر-
بتن).
یک مهندس با تجربه میتواند طراحی سازه های مختلف و پیچیده مثل ساختمانهای بلند مرتبه(مثل
آسمان خراش) و یا
پل را انجام دهد.
بارها در ساختمانها بطور کلی طیقه بندی میشود به بارهای زنده نظیر وزن لوازم و وسائل منزل و مبلمان در ساختمان،نیروهای باد و
وزن آب و نیروهای بوجود آمده بر اثر زلزله، و یا بارهای مرده نظیر وزن خود ساختمان.
بصورت مرسوم، مهندسی سازه براحتی و سادگی در جائی که محورهای متناسب و عمود بر هم باشند عمل می نمایند و برای ساده نمودن معادلات و روابط پیچیده بدست آمده با مقادیر کششی مثل تنش و تغییر مکان های اجزاء بدست آمده سازه، مانند طراحی
تیر ها استفاد میشود.
این ساده سازی جهت توانائی حل مسائل اساسی می باشد. یک مهندس موفق می بایستی سازه را جهت بارهائی که بر روی ساختمان قرار می گیرد به طریقی طراحی کند که تا زمانی که مقدار بار از بار طراحی ، تجاوز ننموده ساختمان
حالت ارتجاعی داشته باشد و وقتی که باربرداشته شودردوباره به حالت اولیه بازگشته و بصورت پایدار باقی بماند.
توسعه و پیشرفت برنامه های کامپیوتری اجازه میدهد بسیاری از محاسبات پیچیده سازه ای با دقت بسیار و سرعت زیاد انجام شود .
یکی از مهمترین مکانیزم های آنالیز های سازه ها روش معادل استاتیکی با قانون حرکت نیوتون که جهت تعیین نیرو های داخلی وارده بر روی اجزاء سازه، استفاده میشود با فرض کلی اینکه مصالح تشکیل دهنده یکنواخت و غیر قابل تغییر شکل میباشد.
مکانیزم و روش دیگری که قادر است به روش کاملتری و در حالات بیشتری عمل نماید روش اجزاء محدود می باشد که امکان محاسبه نیروهای داخلی در سازه و ساختمان با مصالح مختلف و خواص متفاوت را میدهد.
همچنین می بینید:
- طراحی ساختمان
- آنالیز ساختمان
- مهندسی سیویل
- مهندسی مکانیک
- دینامیک
- استاتیک
در استفاده و تعاریف جدید،
مهندسی عمران شاخه ای از مهندسی است که معادل و همراه است با
طراحی،ساخت و نگهداری از
سازه های ساخته شده ای که با زمین و یا با آب و نیز فرهنگ و زندگی شهری و مراحل
تکامل آن ارتباط دارند. امروزه بیشتر مهندسین عمران با
جاده ها،
سازه ها، انتقال آب و سیستم های
فاضلاب،
کنترل سیلاب و
ترافیک سرو کار دارند.
توسعه و پیشرفت مهندسی براساس مشاهدات روش های طبیعی و عکس العمل سیستم های ساخته شده انسانی بوده و پیشرفت و توسعه معادلات تجربی پایه و اساس طزاحی و مهندسی را فراهم نموده است. مهندسی عمران وسیع ترین و گسترده ترین رشته مهندسی می باشد. در حقیقت رشته مهندسی در ابتدا به دو قسمت
نظامی و
عمران تقسیم میگردد. تمامی تخصص های مهندسی عمران بدست آمده است. مهندسی عمران هنوز مانند یک چتری است که بسیاری از تخصص های وابسته به آن را در بر دارد.
زیر شاخه های مهندسی عمران
مهندسی عمران عمومی
مهندسی عمران عمومی راجع به کلیه مواردی که در ارتباط و رابطه متقابل
پروژه های معین و ثابت با
مقیاس وسیعتر می باشد .
مهندسین عمران عمومی به طور نزدیک با نقشه بردارها، مهندسین متخصص عمران کار می کنند. جهت تطبیق دادن و متناسب نمودن محل تحویل شده در پروژه های معین، ترکیب عوارض زمین بوسیله طراحی
شیب بندی و هموار کردن آن (grading) ، انتقال
آبهای سطحی و (کنترل طغیان و سیلابها)، تهیه پوشش و روکش ها و انتقال آب، سیستم جمع آوری و دفع
فاضلاب،
برق و
مخابرات و
تفکیک اراضی.
مهندسین عمومی جهت بازدید از محل پروژه ها، توسعه و پرورش مالکیت های مشترک و توافق همسایگان و تهیه طرح های ساختمانی وقت زیادی را صرف می نمایند.
مهندسی سازه
مهندسی سازه در ارتباط با طراحی پل ها، ساختمان ها ساخت تاسیسات نفتی روی خشکی، سد ها و غیره می باشد اجزاء تشکیل دهنده مهندسی ساختمان طراحی و آنالیز سازه می باشد و کلیه مراحل طراحی ساختمان هستند. این شامل محاسبه تنش ها و نیرو های فعال در ساختمان می شود.
بعضی از مهندسین ساختمان در بخش و زمینه های گوناگون و متفاوت دیگر مشغول بکار می باشد از قبیل طراحی
هواپیما و
فضا پیما و حتی وسائل پزشکی.
مهندسی ژئوتکنیک
مبحث مهندسی ژئو تکنیک پایه و اساس
مهندسی سازه میباشد.
در خصوص اهمیت مهندسی ژئو تکنیک به سختی می توان اغراق نمود، زیرا
ساختمان و سازه بایستی در ارتباط مستقیم با زمینی که برو روی آن قرار می گیرد باشد. مهندسی ژئو تکنیک به خصوصیات و مشخصات خاک و فونداسیون و پی و دینامیک خاک بستگی دارد.
مهندسی حمل و نقل
مهندسی حمل و نقل در ارتباط با
تئوری صف بندی، جریان حرکت ترافیک، طرح هندسی راه و رفتار رانندگان می باشد.عملکرد و نمود فعالیت ترافیک ازمیان استفاده مصرف سفرهای تولید شده و نیز خصوصیات و مشخصات و محاسبه عددی ترافیک تعیین می گردد که با محاسبات پیچیده ای برای حل مسائل ترافیک مواجه می باشد.
مهندسی محیط زیست
مهندسی محیط زیست در ارتباط است با عملکرد
مواد شیمیایی و
زیست شناسی موجودات و یا اتلاف
گرما و
انرژی حرارتی،
تصفیه و پالایش آب و هوا و اصلاح و بهبود محل و مکان هائی که در اثر ضرر و زیان های قبلی صدمه دیده اند.
موضوعات تحت پوشش مهندسی محیط زیست عبارتند از:
تصفیه آب،
دفع فاضلاب،مدیریت خسارات و صدمات و آسیب های پر خطر. مهندسی محیط زیست ارتباط دارد با
هیدرولوژی و
علم هواشناسی تا جائیکه دانش راجع به آب و جریانات و دانستن چگونگی انتقال آلوده کننده ها احتیاج و نیاز می باشد. مهندسی محیط زیست همچنین شامل واکنش و مقابله در برابر آلودگی صنعتی میباشد. مهندسی محیط زیست بخش پیشرفته و مدرن
بهداشت است.
چندین بخش دیگر که استفاده میشود عبارتند از:
مهندسی سلامت جامعه و
مهندسی سلامت محیط زیست.
مهندسی هیدرولیک
مهندسی هیدرولیک مبحث مرتبط با حرکت و انتقال مایعات و بطور اخص آب است.
این مبحث مهندسی بطور یقین ارتباط با طراحی
پل ها،
سدها،
کانال ها،
اسکله ها پیدا می کند و همچنین ارتباط با هر دو موضوع مهندسی محیط زیست و بهداشت را نیز دارد.
علم مواد
همچنین مهندسی عمران شامل مهندسی علم مواد نیز شامل میشود. مهندس مواد با پتانسیل های که در کار مهندسی ایجاد شده شناخت
بتن و
فولاد و اخیرا
پلیمرها و
سرامیک ها را شامل میگردد.
Careers«مسیرها _ راه ها )
یک ذهنیت و تصور نادرست اینست که مهندسی عمران از
مرزها و محدوده
ریاضیات و
علوم رایانه دور است. در حقیقت بسیاری از آنچه هم اکنون در علم رایانه وجود دارد ناشی از کار و فعالیت در رشته مهندسی ساختمان است، در جائی که مهندسی سازه و مسائل
آنالیز شبکه ها به معادلات موازی احتیاج دارد. همچنین مهندسین عمرانی وجود دارند که در رشته
مهندسی ایمنی، تهیه روش های آماری جهت طراحی ساختمان و سازه ها، آنالیز ایمنی و فنی تخمین خسارات بیمه ای بر اساس اتفاقات طبیعی وخطرات انسانی به وجود آمده کار می کنند.
مکانیک خاک
دید کلی
در
علوم مهندسی ، خاک مخلوط غیر یکپارچهای از دانههای کانیها و
مواد آلی فاسد شده میباشد که فضای خالی بین آنها توسط آب و هوا (گازها) اشغال شده است.
خاک به عنوان مصالح ساختمانی در طرحهای مهمی در
مهندسی عمران بکار گرفته میشود و همچنین شالوده اکثر سازهها بر روی آن متکی است.
بنابراین مهندسان عمران باید بخوبی خواص خاک از قبیل مبدا پیدایش ،
دانه بندی ،
قابلیت زهکشی آب ، نشست ،
مقاومت برشی ، ظرفیت باربری و غیره را مطالعه نمایند. مکانیک خاک شاخهای از علوم مهندسی است که به مطالعه مشخصات فیزیکی و رفتار توده خاکی تحت بارهای وارده میپردازد.
مهندسی پی ، کاربرد اصول مکانیک خاک در مسائل عملی است.
تاریخچه
تاریخچه عملیات خاکی را میتوان به دورههای دور تاریخ بشری نسبت داد و آن را با قدمت
پیدایش شهرنشینی یکی دانست.
حفر قناتها ، کانالهای آبرسانی ، ایجاد پلها و سدهای محکم و سایر بناهایی که آثار آنها در کشورهای دنیا از دهها قرن قبل تا کنون به یادگار مانده است، همه از مواردی است که به نحوی با عملیات خاکی ارتباط دارد.
سیر تحولی و رشد
توجه به بررسی و مطالعه خاک با یک دیدگاه مهندسی و به منظور تحلیل ریاضی خواص آن ، از قرن 18 میلادی آغاز شد و در واقع اولین بار در عین حال مهمترین رابطه ساده در زمینه مکانیک خاک ، در سال 1773 توسط کولمب یک مهندس ارتشی فرانسه ارائه گردید. این رابطه ساده ، که یک رابطه اساسی در بررسی مقاومت یا عدم
مقاومت خاک است عبارت است از:
(τ=c+bntan(φ
کارهای
بوسینسک در مورد تئوری
اجسام الاستیک که در سال 1885 انتشار یافت به ارائه راه حلهای دقیق در محاسبه تنشها و تغییر شکلهای درون محیط خاکی منجر گردید و توانست در تحلیل بخش مهمی از مبحث مکانیک خاک ، پاسخگو باشد. دانش مکانیک خاک به صورت مدرن ، در ابتدای قرن حاضر گسترش روز افزونی یافت و مانند سایر علوم مهندسی مورد تجزیه و تحلیل قرار گرفت بطوری که در سال 1925
کارل ترزاگی ، استاد
دانشگاه هاروارد ، نتیجه تحقیقات خود را به صورت مقالهای ارائه داد و در سال 1943 کتاب «
اصول نظری مکانیک خاک» را تدوین و منتشر کرد.
کارل ترزاگی (1963-1883) را به حق بنیانگذار دانش مکانیک خاک نامیدهاند. در اینجا شایسته است از سهم محققین روسی نیز یادآور گردد، چه پژوهشگرانی چون
سیتوویچ در کشور روسیه به موازات دانشمندان غربی در توسعه دادن مبحث مکانیک خاک کارهای زیادی ارائه دادند. نامبرده نیز در سال 1934 کتاب
اصول علم مکانیک خاک را منتشر نمود.
امروزه اهمیت دانش مکانیک خاک مانند علوم دیگر روز به روز رو به فزونی است و این بویژه به این علت است که تجربههای گذشته در این زمینه بدون گسترش تئوریهای مطمئنتر و راه حلهای اقتصادیتر تکافوی حل مسائل جدید را در عمل نمینماید. به علاوه ، بسط مسائل مبحث مکانیک خاک همراه با توسعه روشها و دیدگاههای جدید در زمینه مکانیک محیط دانهای ، گسترش و افزایش دقت در تحلیلهای ریاضی و مدل سازیها را در هر دو زمینه الزامی نموده و نیز به نتیجه رسانده است.
مباحث کلی مکانیک خاک
- طرح تئوریهایی که نشان دهنده رفتار توده خاکی در برابر عوامل بیرونی ، مثل نیروهای مختلف ، باشد.
- کاربرد معلومات تئوری و تجربی در موارد و مسائل اجرایی
خواص فیزیکی ، شیمیایی و کانی شناسی خاکها
- خواص فیزیکی و شیمیایی خاک : شناخت خواص فیزیکی ، شیمیایی و کانی شناسی خاکها در بسیاری از بررسیها و مطالعات و تصمیم گیریها در عملیات خاکی نقش مهمی دارد. خواص فیزیکی و شیمیایی خاکها را باید عمدتا در عوامل زیر جستجو کرده و مربوط به آنها دانست.
- ترکیب کانی شناسی دانهها : از آنجایی که خاکها از تجزیه و هوازدگی سنگهای پوسته زمین پدید آمده است، لذا کانیهای تشکیل دهنده خاکها باید همان کانیهای تشکیل دهنده سنگ مادر باشد.
- طبیعت سطح ذرات خاک (سطح مخصوص) : سطح خارجی دانههای خاک ، یعنی فصل مشترک محیط جامد با محیط مجاور آن که ممکن است، آب یا هوا باشد. محل پدید آمدن بعضی پدیدههای فیزیکی یا شیمیایی است که این پدیدهها برخواص دیگر خاک مثل؛ مقاومت و نفوذپذیری و ... تاثیر میگذارد.
- پدیدههای فیزیکی و شیمیایی در سطح مشترک خاک و آب :ذرات جسم جامد از شبکهای از یونهای مختلف تشکیل شده است که از اینرو بین سطح خارجی ذره و محیط اطراف آن کنش و واکنشهایی پدیدار میگردد.
- خاصیت مویینگی : خاصیت بالا رفتن آب در لولههای مویین و در حفرههای بین ذرات خاک را خاصیت مویینگی گویند.
- نیروهای دافعه و جاذبه بین ذرات : نیروهای بین ذرهای در خاک به دو گونهاند. نیروهای جاذبه مولکولی بین دانهها (وان در والس) و نیروهای دافعه که از نوع نیروی الکتروکینیماتیکی است.
خواص مکانیکی خاکها
- اصطکاک : مقاومت جسم در برابر حرکت به علت وجود اصطکاک بین دو سطح تماس است.
- چسبندگی: مقاومت خاکی به علت چسبندگی دانهها حاصل از مقاومت مولکولی (یعنی نیروی جاذیه الکتروشیمیایی) بین ذرات ریز است.
- گسیختگی توده خاک : گسیختگی توده خاک عبارتست از پایان شرایط مقاومت و آغاز برش در خاک است.
- تحکیم: تحکیم عبارتست از کاهش حجم حفرههای آبدار درون خاک به علت افزایش فشارهای جانبی.
کاربرد مکانیک خاک
خاک از یک طرف به عنوان مصالح مورد توجه مهندسین و طراحان قرار میگیرد و از سوی دیگر به عنوان یک محیط طبیعی که در اختیار آدمی قرار گرفته است مورد توجه و استفاده است. جایی که به عنوان مصالح مورد نظر است مانند خاکریزها ، سرای خاکی ،
روسازی راه و فرودگاه ، پشت
دیوار حایل ، زهکشها ، و به عنوان بخشی از
بتن ، ماده اصلی تهیه
آجر و
سرامیک ، ماده اصلی تهیه
چینی و
کاشی ، و... حالت انتخابی و اختیاری دارد، و در جایی که به عنوان محیط مورد توجه است.
مانند زیر پیها ، زیر پایه پلها و زیربنای جادهها و محل حفر تونلها و محل قرار دادن لولهها و تاسیسات مکانیکی و الکتریکی (کابل های تلفن و برق و
لوله کشی گاز و
فاضلاب و محل احداث قناتها و محل حفر چاهها و کانالها و ... همه حالت غیر انتخابی (یعنی اجباری) دارد. به هر حال در تمام موارد ذکر شده ، شناخت خواص فیزیکی و مکانیکی خاک ضرورت غیر قابل اجتناب دارد. مثلا در یک
پروژه راه سازی ، چه نوع
خاکی با چه نوع
دانه بندی باید انتخاب شود و لایههای آن با چه ضخامتی و با چه رطوبتی و تا چه حد باید کوبیده شود تا جایی حاصل بتواند در برابر نیروهای وارد بر آن مقاوم باشد و وجود آبهای سطحی و بارندگی بر دوام آن اثر مخرب نداشته باشد و در برابر یخزدگی و
فرسایش و تغییرات جوی نیز پایدار بماند.
در ایجاد یک
سد خاکی ، شیبها چه مقدار باشد که هم پایدار باشد و هم اقتصادی ، در صورتی که سد همگن با
زهکشی است، لایههای زهکشی با چه ابعادی و با چه دانه بندی و چه مقدار نفوذپذیری باید باشد؟
سرعت حرکت آب و .... زه چه مقدار است؟ تورم یا نشست خاک چه مقدار باشد؟ میزان تراکم و درصد رطوبت و ضخامت لایهها برای کمپاکت کردن خاک چه مقدار باید باشد؟ روشهای حفاظت دامنهها و تاج سر به چه عواملی بستگی دارد؟ و بسیاری پرسشهای دیگر که مهندس طراح باید برای آنها جواب دقیق داشته باشد. به این ترتیب درمورد هرگونه پروژه ساختمانی و راه سازی و
سد سازی مسائل متعددی از
فیزیک و مکانیک خاک باید پاسخ داده شود. اهمیت دقت بیشتر و نیاز به تئوریهای دقیقتر هنگامی بیشتر میشود که حجم کارها و اهمیت پروژه بیشتر باشد.
رابطه مکانیک خاک با سایر علوم
مبحث مکانیک
خاک دانشی است که در آن خواص فیزیکی و مکانیکی خاکها ، ارتباط این خواص با عوامل بیرونی ،
مقاومت در برابر نیروها ، تغییر شکل خاک در اثر نیروها ، مسایل مربوط به حرکت یا سکون آب در خاک ، چگونگی و مقدار فشرده شدن خاکها و چگونگی و مقدار تنشها و تغییر شکلهای هر نقطه از محیط خاکی در اثر عملکرد یک نیروی خارجی و ... بحث میشود.
در این راستا گاهی نیاز به مطالعه خواص شیمیایی و
کانی شناسی دانههای خاک است و گاهی نیاز به بررسی
پیدایش و منشا خاکها و گاهی نیاز به استفاده از دانش هیدرولیک و دانشهای دیگر است. از اینرو ارتباط این مبحث با دیگر مباحث علمی چون
فیزیک ،
شیمی ،
زمین شناسی ،
کانی شناسی ،
هیدرولیک و
مکانیک سیالات را نباید از نظر دور داشت.
مباحث مرتبط با عنوان
فرآیندهای تشکیل انواع خاک
دید کلی
فرآیندهای شیمیایی و فیزیکی متعددی در تشکیل انواع مختلف خاک نقش دارند. در طی فرآیندهای شیمیایی ، مواد معدنی و آلی دچار تجزیه و تغییر میشوند و در ضمن فرآیندهای فیزیکی ، مواد حاصل جابجا شده و
افقهای مختلف خاک را حاصل میآورند.
تشکیل خاک خاکستری یا سفید (podsolization یا Spodsolization)
این مورد فرآیندی از شکل گیری خاک است که در آن آهن و آلومینیوم از افقهای A و E شسته شده و در افق B متمرکز میشوند. این فرآیند در اقلیمهای مرطوب دیده میشود. فصل زمستان ، روند تجزیه مواد آلی در سطح خاک و ریشه گیاهان را که منطقه بقایای مواد آلی است، آهسته میکند. بعضی از اکسیدهای آهن و آلومینیوم به همراه رس و کلوئیدهای هوموس ، در افق B جمع میشود (منطقه رسوبگذاری) و به این افق بافتی رسی میدهند.
آب موجود در خاک ، هیدروکسیدهای سدیم ، کلسیم ، منیزیم و پتاسیم محلول را به وسیله
آبهای زیرزمینی از منطقه نشت و شستشو میدهد. نتیجه این شستشو ، اسیدی شدن آب است. فرآیند تشکیل خاک با تغییر آب و هوا دگرگون میشود و با گرمتر شدن هوا
spodosol به AlFisol و uLtisol تبدیل میشود.
البته این فرآیندها قبل از
پدیده لاتریت زایی (Oxisolation) در مناطق حاره روی میدهد. جنگلهای ایالات متحده و کانادا معمولا بطور طبیعی دارای
خاک اسپادوسول (خاک خاکستری یا سفید) هستند.
لاتریت زایی (Oxisolation)
این فرآیند زمانی رخ میدهد که آهن و آلومینیوم اکسید شده و لایهای از مواد قرمز با بافت گرهی سخت کوچک (گرهک) که
لاتریت نامیده میشود، در افق B بوجود میآید. این فرایند اغلب در مناطق حاره دیده میشود. در مناطق گرم و مرطوبی که گرم و خشک شدن بطور متناوب صورت میگیرد، این عمل برای اکسیداسیون فلز آهن بسیار مطلوب است.
خاک افق B ، رنگ قرمز تیره اکسیدهای آهن را به خود میگیرد. در این افق ، اکسیدهای آهن و آلومینیوم و کانیهای رسی با هم تجمع میکنند (
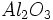
و
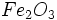
). به دلیل رطوبت ، سدیم ، کلسیم ، منیزیم و پتاسیم در آب زیرزمینی حل و برای ریشههای گیاهان غیر قابل دسترس میشوند. به دلیل آزاد بودن یون هیدروژن ، خاکهای لاتریتی بسیار اسیدی هستند.
جنگلهای استوایی (حارهای) مکزیک و هاوایی خاکهای لاتریتی دارند.
کلسیتی شدن (Caicification)
این فرآیند زمانی رخ میدهد که آب درون خاک به شدت تبخیر میشود و کسری بودجه سالانه آب بوجود میآید. در بیابانهای داغ و اقلیمی استپی ، این فرآیند دیده میشود. نزولات آسمانی در این مناطق به قدری کم است که نمیتواند هیدروکسیدهای کلسیم ، سدیم ، منیزیم و پتاسیم را بشوید و آن را به افق پایین خاک ببرد.
آب موجود در خاک به دلیل تبخیر از طریق لولههای موئینه (Capillary) به سطح خاک کشیده میشود. تکرار این محل موجب میشود که برآمدگیهای کوچک کربنات کلسیم در افق B بوجود آید.
نمک زائی (Salinization)
گرمتر شدن اقلیم ، فرآیند کلسیتی شدن را در مناطق بسیار خشک به نمک زائی تبدیل میکند و تمام سطح خاک پوشیده از نمک میشود. خاکهای کلسیتی شده (Calcified) ، معمولا PH نزدیک به خنثی دارند (6،5 تا 8). به دلیل تامین مواد مغذی (هیدروکسیدها) ، این خاکها اگر آبیاری شوند، محصول زیادی را به بار میآورند. در
خاکهای سالین یا
نمکی فقط گیاهان نمک دوست رشد میکنند.
تشکیل خاک رس (Gleization)
تشکیل خاک رس ، فرآیند دیگری از شکل گیری خاک است که وقتی ترکیب چسبنده آبی مایل به خاکستری رس و
هوموس که
Cley نامیده میشود، در افق B تجمع مییابد، بوجود میآید.
نقش اقلیمهای مختلف در تشکیل خاک رس
این فرآیند در اقلیمهای آبی به دلیل اینکه برای استقرار و ثبات به آب نیاز دارد و در اقلیمهای تندرا به علت تقسیم شرایط مطلوب ، صورت میگیرد. در اقلیمهای دیگر نیز این فرآیند بوجود میآید، برای مثال اگر آب در افق B و C تندرا (Tundra) در یک دوره طولانی تجمع پیدا کند. این حالت زمانی رخ میدهد که به دلیل شرایط زمین شناختی برکهها (آبگیرها) یا لایه رس قوی افق B ، به یک بند تبدیل میشود و آب به داخل خاک تراوش میکند.
اقلیمهای ایدهآل برای تشکیل خاک رس
نواحی مرطوب ساحلی و باتلاقها ، شرایط مناسبی را برای فرآیند Gleization فراهم میسازند. اقلیمهای تندرا نیز به دلیل وجود خاک یخ زده ، برای این فرآیند ایدهآل است.
نقش حوضچه و یا آبگیر در تشکیل خاک رس
در بهار ، یخ موجود در سطح خاک ذوب میشود و در بالای خاک یخ زده یک حوضچه ایجاد میکند، همچون یک آب بند عمل میکند. حوضچه و یا
موضوع: <-PostCategory->
جمعه 14 شهريور 1391برچسب:, 13:15
 |
پلهای بتن مسلح به اشکال مختلف به صورت پلهای قوسی، پل های صفحه ای (پل دال)، پل با تیرهای حمال (مقطع تیرو تاوه)، پلهای جعبه ای و پلهای قابی شکل ساخته می شوند این پلها رامی توان به صورت پیش ساخته یا ساخته شده در محل (بتن ریزی در جا) با مقطع ثابت یا متغیر و به صورت دهانه ساده یا یکسره ساخت.
درمورد دهانه های کوچک (کمتراز 10متر) استفاده از پلهای صفحه ای (دال توپریا توخالی ) بسیار معمول است برای دهانه های بزرگتر نیز عموماً از پل باتیرهای حمال استفاده می شود در این حالت فرم مقطع به شکلTو I یا T دوبل است.
در حالت پیش ساختگی گاهی جان و قسمتی از بال به صورت پیش ساخته آماده و نصب شده و سپس قسمت باقیمانده دال در محل بتن ریزی می شود.
در مورد پل های چند دهانه می توان تیرها را با قراردادن درزهائی در امتداد تکیه گاه ها از هم جدانمود که در نتیجه به صورت ایزواستاتیک (روی تکیه گاه ساده) عمل می کنند در حالت پلهای یکسره معمولا ارتفاع مقطع دارای تغییرات سهمی یا خطی بوده و یا در صورت ثابت بودن مقطع می توان آنها را درروی پایه ها با قراردادن ماهیچه تقویت نمود.
معمولا این نوع پلها برای دهانه های تا 30متر ساخته شده و برای دهانه های بزرگتر استفاده از پلهای بتن پیش تنیده باصرفه تر می باشد.تیرهای پل با واسطه صفحات تکیه گاهی روی پایه ها قرارمی گیرند.
پلها را از نقطه نظر مصالح تشکیل دهنده به شکل زیر طبقه بندی می کنند.
طبقه بندی پلها از نقطه نظر مصالح تشکیل دهنده:
این پلها معمولا" به شکل قوسی، با تیرهای مشبک و یا تیرهای حمال ساخته شده و در حال حاضر استفاده از آنهابه صورت موقتی می باشد.
با توجه به مقاومت مناسب فشاری مصالح سنگی، بسیاری از پلهای طاقی از این مصالح ساخته شده اند.نظر به کمبود افراد سنگ کار و زمان نسبتا طولانی لازم برای تهیه مصالح و اجرای سازه، امروزه استفاده از این پلها محدود می باشد.
در بسیاری از پلهای طاقی شکل، در حال حاضر از بتن، با توجه به مقاومت فشاری مطلوب آن به جای سنگ استفاده می شود.
با توجه به روش اجرا و نحوه بتن ریزی، پلهای بتن مصلح را می توان از مقاطع مختلف و با اشکال دلخواه ساخت. با وجود این استفاده از مقاطع ساده در جهت کاهش بهای قالب بندی همواره مورد نظر است.در بعضی از حالات استفاده از سیستم پیش ساختگی باعث حذف اجزاء نگهدارنده قالبها و در نتیجه صرفه جوئی قابل ملاحظه می شود.
با پیشرفت این تکنیک، به تدریج در دامنه وسیعی از ابنیه فنی،پلهای بتن پیش تنیده جایگزین پلهای فلزی و پلهای بتن مسلح شده اند. بدین ترتیب با صرف هزینه کمتر، پلهای با دهانه بزرگ ساخته می شوند. از طرف دیگر استفاده از این مصالح امکان به کارگیری تکنیک های جدید پل سازی را می دهد.
این پلها به اشکال مختلف، با تیرهای حمال معمولی یا تیرهای مشبک فولادی، با قوس یا قالبهای فلزی، نورد شده از ورق و المانهای اتصالی ساخته شده اند. در ساخت این پلها گاهی نیز از آلیاژهای سبک یا مقطع مرکب استفاده می گردد.
پل یک سازه است که برای عبور از موانع فیزیکی از جمله رودخانه ها و دره ها استفاده می شود.پلهای متحرک نیز جهت عبور کشتیها و قایقهای بلند از زیر آنها ساخته شده است.
تاریخچه پل
ایجاد گدرگاهها وپلها برای عبور از
دره ها و
رودخانه ها از قدیمی ترین فعالیتهای بشر است. پلهای قدیمی معمولا از
مصالح موجود در طبیعت مثل
چوب و
سنگ والیاف گیاهی به صورت معلق یا با تیرهای حمال ساخته شده اند.
پلهای معلق از
کابلهایی از جنس الیاف گیاهی که از دو طرف به تخته سنگها و درختها بسته شده و پلهای با
تیر حمال از
تیرهای چوبی که روی آنها با مصالح سنگی پوشیده می شد، ساخته شده اند.
ساخت پلهای سنگی به دوران قبل از رومیها بر می گردد که در
خاور میانه و
چین پلهای زیادی بدین شکل برپا شده است. در
اروپا نیز اولین
پلهای طاقی را 800 سال قبل از میلاد مسیح، برای عبور از رودخانه ها از جنس مصالح سنگی ساخته اند.اغلب پلهای ساخته شده توسط رومیها از طاقهای سنگی دایره شکل با پایه های ضخیم تشکیل یافته است.در ایران نیز ساختن پلهای کوچک وبزرگ از زمانهای بسیار قدیم رواج داشته و پلهایی نظیر سی و سه پل، پل خواجو وپل کرخه بیش از 400 سال عمر دارند.
از قرن یازدهم به بعد روشهای ساختن پلها پیشرفت قابل توجهی نمود و به تدریج استفاده از دستگاههای فشاری از
مصالح سنگی و آجر با
ملاتهای مختلف و
دستگاههای خمشی از چوب متداول گردیده و تا اوایل قرن بیستم ادامه یافت. شروع قرن بیستم همراه با استفاده وسیع از
پلهای فلزی و سپس پلهای بتن مسلح می باشد.
از اوایل قرن نوزدهم ساخت
پلهای معلق، قوسی یا با تیر حمال از
آهن آغاز شد. اولین پل معلق از آهن در سال 1796 به دهانه 21 متر در
آمریکا ساخته شد، همچنین در سال 1850 یکی از مهمترین پلهای با تیر حمال از جنس آهن متشکل از دو دهانه 140 متر و دو
دهانه 70 متری در
انگلستان ساخته شد.
طویل ترین پل معلق به طول تقریبی 7 کیلومتر در
سانفرانسیسکو ساخته و بزرگترین دهانه معلق به طول تقریبی 1400 متر در انگلیس (روی رودخانه هامبر) طراحی شده اند. در سالهای اخیر طرح پلهای ترکه ای فلزی (با کابل مستقیم) نیز برای دهانه های بزرگ مورد توجه قرار گرفته و بعد از نخستین پل که در سال 1955 به دهانه 183 متر در سوئد ساخته شده، پلهای زیادی اجرا شده است.
طبقه بندی پلها:
پلها را می توان ازنقطه نظرهای مختلف طبقه بندی نمود:
همچنین ببینید
با توجه به مخارج سنگین انجام شده برای اجرای ابنیه
بتنی،مسئله نگهداری دقیق این سازه ها در برابر آب و باد دو یخبندان از اهمیت خاصی بر خوردار است.
در مناطقی که بستر رودخانه سست بوده و در اثر طغیان آب امکان شسته شدن داشته باشد باید وضعیت آن را در اطراف پل بعد از طغیانهای مختلف مورد برسی قرار داد تا با تدابیر مختلف از خالی شدن خاک اطراف پی ها و در نتیجه تخریب پایه ها جلوگیری شود.
لایه
عایق کاری و اسفالت کف جاده باید طوری انجام شود که از نفوذ و باقی ماندن آب در جسم پل جلوگیری شود.
بعد از پایان ساختمان
پل و قبل از تحت سرویس قرار گرفتن،المانهای مختلف آنرا باید به دقت مورد بازدید قرار داد تا مشخص شود تحت
بارهای دائمی و دستگاههای ساخت،تغییر شکل ها و ترک های پیش بینی نشده در آن ایجاد نشده باشد، همچنین بعد از آزمون
بار گذاری که تحت شدید ترین بارگذاری ممکنه در طول دوره سرویس قرار می گیرد، باید کلیه تغییر شکلهای ایجاد شده و فلش مقاطع بحرانی، ترک های احتمالی، نشست پایه ها، تغییر فرم
دستگاههای تکیه گاهی و اتصالات مختلف به دقت مورد برسی قرار گیرند.
در طول دوره بهره برداری نیز در زمانهای مشخص باید قسمتهای مختلف پل مورد بازدید قرار گیرند به عنوان مثال:در
پلهای فلزی که احتمال از بین رفتن اتصالات پیچ و جوش، زنگ زدن المانها و خوردگی آنها و بروز نا پایداریهای الاسیتک موجود است. این بازدیدها باید به طور مداوم و حداقل هر پنج سال یکبار انجام شده و برای جلو گیری از تخریب قطعات، آنها را با مواد مناسب پوشانید. همجنین در مورد
پلهای بتن پیش تنیده شده وضع دستگاههای مهارتی و کشش کابلها مورد بررسی قرار گرفته و با انجام عمل تزریق به نحو مناسب، از زنگ زدگی کابلها جلوگیری به عمل آید.
از عبور سربارهای غیر مجاز که در طرح ومحاسبه قطعات پل در نظر گرفته نشده اند،اکیدآ جلوگیری شود.
موضوع: <-PostCategory->
دو شنبه 10 شهريور 1391برچسب:, 23:12
از نامگذاری «مثلثات» می توان حدس زد كه این شاخه از ریاضیات دست كم در آغاز پیدایش خود به نحوی با «مثلث» و مسئله های مربوط به مثلث بستگی داشته است. در واقع پیدایش و پیشرفت مثلثات را باید نتیجه ای از تلاش های ریاضیدانان برای رفع دشواری های مربوط به محاسبه هایی دانست كه در هندسه روبه روی دانشمندان بوده است.
تاریخ علم به آدمی یاری می رساند تا «دانش» را از «شبه دانش» و «درست» را از «نادرست» تشخیص دهد و در بند خرافه و موهومات گرفتار نشود. در میان تاریخ علم، تاریخ ریاضیات و سرگذشت آن در بین اقوام مختلف ، مهجور واقع شده و به رغم اهمیت زیاد، از آن غافل مانده اند. در نظر داریم در این فضای اندك و در حد وسعمان برخی از حقایق تاریخی( به خصوص در مورد رشته ریاضیات) را برایتان روشن و اهمیت زیاد ریاضی و تاریخ آن را در زندگی روزمره بیان كنیم.
برای بسیاری از افراد پرسش هایی پیش می آید كه پاسخی برای آن ندارند: چه شده است كه محیط دایره یا زاویه را با درجه و دقیقه و ثانیه و بخشهای شصت شصتی اندازه می گیرند؟ چرا ریاضیات با كمیت های ثابت ادامه نیافت و به ریاضیات با كمیت های متغیر روی آوردند؟ مفهوم تغییر مبناها در عدد نویسی و عدد شماری از كجا و به چه مناسبت آغاز شد؟ یا چرا در سراسر جهان عدد نویسی در مبنای ۱۰ را پذیرفته اند، با اینكه برای نمونه عدد نویسی در مبنای ۱۲ می تواند به ساده تر شدن محاسبه ها كمك كند؟ ریاضیات از چه بحران هایی گذشته و چگونه راه خود را به جلو گشوده است؟ چرا جبر جانشین حساب شد، چه ضرورت هایی موجب پیدایش چندجمله ای های جبری و معادله شد؟ و... برای یافتن پاسخ های این سئوالات و هزاران سئوال مشابه دیگر در كلیه رشته ها، تلاش می كنیم راه را نشان دهیم، پیمودن آن با شماست...
● پیدایش مثلثات
از نامگذاری «مثلثات» می توان حدس زد كه این شاخه از ریاضیات دست كم در آغاز پیدایش خود به نحوی با «مثلث» و مسئله های مربوط به مثلث بستگی داشته است. در واقع پیدایش و پیشرفت مثلثات را باید نتیجه ای از تلاش های ریاضیدانان برای رفع دشواری های مربوط به محاسبه هایی دانست كه در هندسه روبه روی دانشمندان بوده است. در ضمن دشواری های هندسی، خود ناشی از مسئله هایی بوده است كه در اخترشناسی با آن روبه رو می شده اند و بیشتر جنبه محاسبه ای داشته اند. در اخترشناسی اغلب به مسئله هایی بر می خوریم كه برای حل آنها به مثلثات و دستورهای آن نیازمندیم. ساده ترین این مسئله ها، پیدا كردن یك كمان دایره (بر حسب درجه) است، وقتی كه شعاع دایره و طول وتر این كمان معلوم باشد یا برعكس، پیدا كردن طول وتری كه طول شعاع دایره و اندازه كمان معلوم باشد. می دانید سینوس یك كمان از لحاظ قدر مطلق برابر با نصف طول وتر دو برابر آن كمان است. همین تعریف ساده اساس رابطه بین كمان ها و وترها را در دایره تشكیل می دهد و مثلثات هم از همین جا شروع شد.
كهن ترین جدولی كه به ما رسیده است و در آن طول وترهای برخی كمان ها داده شده است متعلق به هیپارك، اخترشناس سده دوم میلادی است و شاید بتوان تنظیم این جدول را نخستین گام در راه پیدایش مثلثات دانست. منه لائوس ریاضیدان و بطلمیوس اخترشناس (هر دو در سده دوم میلادی) نیز در این زمینه نوشته هایی از خود باقی گذاشته اند. ولی همه كارهای ریاضیدانان و اخترشناسان یونانی در درون هندسه انجام گرفت و هرگز به مفهوم های اصلی مثلثات نرسیدند. نخستین گام اصلی به وسیله آریابهاتا، ریاضیدان هندی سده پنجم میلادی برداشته شد كه در واقع تعریفی برای نیم وتر یك كمان _یعنی همان سینوس- داد. از این به بعد به تقریب همه كارهای مربوط به شكل گیری مثلثات (چه در روی صفحه و چه در روی كره) به وسیله دانشمندان ایرانی انجام گرفت. خوارزمی نخستین جدول های سینوسی را تنظیم كرد و پس از او همه ریاضیدانان ایرانی گام هایی در جهت تكمیل این جدول ها و گسترش مفهوم های مثلثاتی برداشتند. مروزی جدول سینوس ها را تقریبا ۳۰ درجه به ۳۰ درجه تنظیم كرد و برای نخستین بار به دلیل نیازهای اخترشناسی مفهوم تانژانت را تعریف كرد. جدی ترین تلاش ها به وسیله ابوریحان بیرونی و ابوالوفای بوزجانی انجام گرفت كه توانستند پیچیده ترین دستورهای مثلثاتی را پیدا كنند و جدول های سینوسی و تانژانتی را با دقت بیشتری تنظیم كنند. ابوالوفا با روش جالبی به یاری نابرابری ها توانست مقدار سینوس كمان ۳۰ دقیقه را پیدا كند و سرانجام خواجه نصیرالدین طوسی با جمع بندی كارهای دانشمندان ایرانی پیش از خود نخستین كتاب مستقل مثلثات را نوشت.
بعد از طوسی، جمشید كاشانی ریاضیدان ایرانی زمان تیموریان با استفاده از روش زیبایی كه برای حل معادله درجه سوم پیدا كرده بود، توانست راهی برای محاسبه سینوس كمان یك درجه با هر دقت دلخواه پیدا كند. پیشرفت بعدی دانش مثلثات از سده پانزدهم میلادی و در اروپای غربی انجام گرفت. یك نمونه از مواردی كه ایرانی بودن این دانش را تا حدودی نشان می دهد از این قرار است: ریاضیدانان ایرانی از واژه «جیب» (واژه عربی به معنی «گریبان») برای سینوس و از واژه «جیب تمام» برای كسینوس استفاده می كردند. وقتی نوشته های ریاضیدانان ایرانی به ویژه خوارزمی به زبان لاتین و زبان های اروپایی ترجمه شد، معنای واژه «جیب» را در زبان خود به جای آن گذاشتند: سینوس.
این واژه در زبان فرانسوی همان معنای جیب عربی را دارد. نخستین ترجمه از نوشته های ریاضیدانان ایرانی كه در آن صحبت از نسبت های مثلثاتی شده است، ترجمه ای بود كه در سده دوازدهم میلادی به وسیله «گرادوس كره مونه سیس» ایتالیایی از عربی به لاتینی انجام گرفت و در آن واژه سینوس را به كار برد. اما درباره ریشه واژه «جیب» دو دیدگاه وجود دارد: «جیا» در زبان سانسكریت به معنای وتر و گاهی «نیم وتر» است. نخستین كتابی كه به وسیله فزازی (یك ریاضیدان ایرانی) به دستور منصور خلیفه عباسی به زبان عربی ترجمه شد، كتابی از نوشته های دانشمندان هندی درباره اخترشناسی بود. مترجم برای حرمت گذاشتن به نویسندگان كتاب، «جیا» را تغییر نمی دهد و تنها برای اینكه در عربی بی معنا نباشد، آن را به صورت «جیب» در می آورد. دیدگاه دوم كه منطقی تر به نظر می آید این است كه در ترجمه از واژه فارسی «جیپ»- بر وزن سیب- استفاده شد كه به معنی «تكه چوب عمود» یا «دیرك» است. نسخه نویسان بعدی كه فارسی را فراموش كرده بودند و معنای «جیپ» را نمی دانستند، آن را «جیب» خواندند كه در عربی معنایی داشته باشد
|
الف) مقدمه
«هندسه بهترین و ساده ترین منطق ها و مناسب ترین طریق پایدار ساختن اندیشه هاست.» «دکتر فضل الله رضا»
علم هندسه مانند همه ی علوم دیگر از مشاهده و تجربه ناشی شده و ارتباط جدی با احتیاجات اقتصادی بشر دارد. کلمه ی «هندسه» یک کلمه ی یونانی و به معنی مساحی(اندازه ی زمین) است. هندسه و مفاهیم آن از طرفی زاییده ی تجربه و احتیاج بشرند و از طرف دیگر درستی آن باز هم در صحنه ی علوم علمی مورد آزمایش و استفاده قرار می گیرد.
باور مردم از زمان یونانیان باستان تا قرن نوزدهم این بود که هندسه ی اقلیدسی، حقیقت محض و بی کاستی است که فضای مادی را بطور کامل توجیه می کند. حتی کانت اعتقاد داشت که هندسه ی اقلیدسی، ذاتی ساختار ذهن انسان است…اما هندسه دانهای قرن نوزدهم نشان دادند که اولا هندسه ی اقلیدسی تنها هندسه ی ممکن نیست، ثانیا این که هندسه فضای مادی اقلیدسی یا نا اقلیدسی است، امری تجربی است که خارج از حیطه ی ریاضیات محض می باشد و ثالثا هندسه ی اقلیدسی سازگارتر است، اگر و فقط اگر هندسه ی نااقلیدسی سازگار باشد یعنی این دو هندسه به بیانی نادقیق«به یک نسبت درستند.»
ب) تاریخچه ی پیدایش هندسه ی نااقلیدسی
در حدود سیصد سال قبل از میلاد، اقلیدس کتاب «مقدمات» خود را به رشته ی تحریر در آورد، او بر اساس پنچ اصل موضوع و تعدادی اصطلاح اولیه تمام هندسه ی شناخته شده تا زمان خود را بصورت دستگاهمند و به روش اصل موضوعی در کتابش ذکر کرد. یکی از اصل های اقلیدس که بیشتر از همه توجه ریاضیدانان را بخود جلب کرد، اصل پنجم این کتاب بود. اقلیدس این اصل را که به «اصل توازی» معروف شده است این طور بیان می دارد:
«اگر خطی دو خط را چنان قطع کند که مجموع زوایای داخلی کتر از دو قائمه باشد، آن گاه دو خط همدیگر را در همان طرف قطع می کنند.»
که بعدها معادل آن یعنی:«از هر نقطه خارج یک خط راست، تنها یک خط راست موازی با آن خط و در همان صفحه ی مفروض میتوان رسم کرد.» تنظیم شد. تلاش برای اثبات این اصل براساس چهار اصل دیگربه بیش از بیست قرن انجامید و در این مدت بنظر می رسید که هندسه با بن بست مواجه شده است. در واقع از همان زمان که کتاب مقدمات اقلیدس نوشته شد، بحث و تفسیر درباره ی آن آغاز گشت، این بحث ها از دو جهت بود:
- برطرف کردن ابهام هایی که در«تعریف ها»، «اصل ها» و «قضیه ها» وجود داشت.
- بحث درباره ی اصل توازی.
اما با وجود اینکه دانشمندان برای اثبات دقیق این اصل با عدم موفقیت های فراوان مواجه شده بودند، باز هم دست از کوشش بر نداشتند دلیل آن این بود که علمای هندسه اعتقاد داشتند که بدون روشن کردن موقعیت این اصل نمی توان ساختمان هندسه را بطور دقیق و کامل انجام داد، این تلاش ها سرانجام به کشف هندسه های نااقلیدسی منجر شد.
می گویند اولین کسی که به استقلال اصل پنجم یا به گفته ی کایزر «مشهورترین تک سخن در تاریخ علم» شک کرد، خود اقلیدس بود. بعد از او بطلمیوس (حدود ۱۵۰ سال پیش از میلاد) برای اثبات آن برخاست. پرودوکلوس نیز در قرن پنجم شرحی بر کتاب اصول نوشت و ضمن نشان دادن اشتباه برهان های قبلی، تلاش کرد تا اثباتی در این زمینه ارائه کند.
بعد از آن شاهد اثبات های دیگری بودیم که هیچ یک به نتیجه ی مطلوب نرسیدند. از جمله دانشمندان ایرانی که برای اثبات این اصل تلاش کرد میتوان به خیام، خواجه نصیر الدین طوسی، نیریزی و ابن هیثم اشاره نمود.
خیام در مقاله ی اول کتاب خود با نام«شرح ما اشکل من مصادرات کتاب اقلیدس»
به مساله ی اصل توازی پرداخت. او میگوید:«اشتباه دانشمندان سابق در این است که بنیان های فلسفی را در نظر نمی گیرند…». او که سخت طرفدار عقاید کانت بود منظور از عقاید فلسفی را همان عقاید کانت میداند و بدان اشاره می کند.
دانشمندان اروپایی نیز برای اثبات این اصل تلاش های در خور توجهی کردند کسانی همانند: جان والیس و جیرولاموساکری.
ساکری در ۱۶۹۷ کتابی با عنوان «اقلیدس مبرا از هر نقص» را ارائه کرد که در آن برای اثبات اصل پنجم که بیشتر به یک قضیه شبیه بود تا اصل، از روش برهان خلف استفاده کرد و سعی کرد تا به تناقض برسد، اما در واقع او هرگز به تناقضی نرسید. شاید اگر ساکری میدانست که به این دلیل ساده به تناقض نمی سد که اصلا تناقضی در کار نیست، کشف هندسه های اقلیدسی نزدیک به یک قرن زودتر صورت می پذیرفت.
اندکی بعد و در قرن ۱۸ و در آلمان لامبرت مانند ساکری با استفاده از برهان خلف سعی کرد اصل توازی را اثبات کند اما او نیز به تناقضی نرسید و در رده ی اثبات کننده گان ناکام این اصل قرار گرفت. چنین می نماید که وی دریافته بود که دلایل علیه بیشتر پی آمد سنت ها و احساسات بودند. او معتقد بود این دلایل از نوعی بودند که بایستی به یکباره از عرصه ی هندسه و نیز از میدان هر علمی بیرون رانده شود.
پژوهش های او درباره ی نظریه ی توازی بوسیله ی رساله ای از آدرین لژاندر طی سال ها کار روی اصل توازی، به مجموعه ای از اثبات های اشتباه دست یافت که از آن ها در کلاس هندسه اش استفاده میکرد اما دو گزاره ی مهم که لژاندر ثابت کرد پایه گذار «هندسه ی مطلق» (یعنی هندسه ی مبتنی بر چهار اصل اول) بود.
اصل توازی آن چنان ذهن او را به خود معطوف داشته بود که طی ۲۹ سال چند بار اصول هندسه اش را تجدید چاپ کرد و هر بار یکی از کوشش های تازه اش در مورد اصل توازی را در آن ارج نمود.
|
دوره دوم تكامل ریاضیات با سمت گیری كاربردی را (كه در ضمن دوره سوم تكامل ریاضیات بود) باید از سده هشتم تا سده شانزدهم میلادی دانست، دوره ای كه گرانیگاه آن در ایران بود. زندگی مسئله های تازه ای را پیش آورد كه باید به یاری ریاضیات حل می شد و ریاضیات نظری دوره پیش (ریاضیات یونانی) از عهده حل آنها بر نمی آمد. این مسئله ها به طور عمده مربوط می شد به اخترشناسی، مكانیك (ساختن ساعت های مكانیكی، اسطرلاب و سایر ابزارهای لازم برای رصد، ظریف تر و دقیق تر كردن وسیله های فلزی، سفالی و...) و مسئله های ناشی از اعتقادهای دینی (پیدا كردن جهت قبله، حل مسئله های مربوط به تقسیم ارث و عمل كردن به وصیت نامه ها، كه گاه بسیار پیچیده بود)، گسترش ارتباط های بازرگانی، ساختن قصرها و پرستشگاه ها، ایجاد كاریزها و آبراه ها و...
و ریاضیات با استفاده از همه دستاوردهای دوره های قبل (و به ویژه ریاضیات یونان و هند) با سمت گیری كاربردی (كه در سطحی بسیار بالاتر از ریاضیات كاربردی دوره قبل از یونان بود)، به تكامل خود ادامه داد. اگر از استثناها بگذریم، همه ریاضیدانان این دوره، از پسران «موسی شاكر» تا «جمشید كاشانی»، ایرانی بوده اند.
وقتی می گوییم ریاضیات این دوره با سمت گیری كاربردی به پیش رفته است به این معنا نیست كه در زمینه ریاضیات نظری كاری انجام نشده است بلكه تنها به این معناست كه عامل اصلی پیشرفت ریاضیات انگیزه بیرونی آن (یعنی زندگی، عمل و نیازهای ناشی از آنها) بوده است.
ریاضیدانان ایرانی این دوره با اطلاع از كارهای یونانیان و هندیان و با استفاده از ذخیره فرهنگی غنی قوم های ساكن ایران تلاش كردند كمبودها و شكاف های نظری ریاضیات یونانی را برطرف كنند.
آنها بارها و بارها «مقدمات» اقلیدوس را به بحث انتقادی كشاندند، روش های بطلمیوسی را كه در «المجسطی» آمده بود، تصحیح كردند و تكامل دادند، پایه های جبر و مثلثات و به طور كلی ریاضیات محاسبه ای را ریختند، با بررسی دقیق مربوط به نسبت ها مفهوم عدد حقیقی را به عنوان یك كمیت پیوسته وارد ریاضیات كردند، پایه های اصلی هندسه نااقلیدوسی را بنا نهادند، روش های ارشمیدس را در زمینه «انتگرال گیری» تكامل بخشیدند و غیره و غیره. ولی در همه این زمینه ها توجه اصلی ریاضیدانان ایرانی، به نیازهای زندگی و دانش های دیگر بوده است. خوارزمی جبر را به دلیل دشواری هایی كه در فقه اسلامی برای تقسیم ارث وجود داشت، پدید آورد. نیمه نخست كتاب «جبر و مقابله» خوارزمی، بحثی نظری درباره راه حل معادله های درجه اول و درجه دوم- هم با محاسبه و هم به كمك استدلال های هندسی- است. البته خوارزمی از نمادهای جبری استفاده نمی كند و مسئله ها را به صورت توصیفی حل می كند، ولی دقت در روش های حل او، ما را به دستوری می رساند كه امروز، برای حل معادله درجه دوم، به كار می بریم.
خوارزمی و ریاضیدانان ایرانی بعد از او، عدد منفی را- جز در برخی حالت های استثنایی- به كار نمی برند، به معادله های بالاتر از درجه سوم توجهی نداشتند (خیام، در كتاب جبر خود، برخی از گونه های معادله درجه سوم را به كمك مقطع های مخروطی حل كرده است) و اغلب تنها به یكی از ریشه های معادله، اكتفا می كردند و همه اینها به دلیل توجه اصلی آنها به عمل و نیازهای زندگی بوده است. به طور مثال، ریاضیدانان ایرانی (به پیروی از ریاضیدانان یونانی)، اگر طول پاره خط راست را برابر a می گرفتند،a۲ را مربعa (یعنی مساحت مربعی به ضلع برابر a) و a۳ را مكعبa (یعنی حجم مكعبی به ضلع برابر a) می گفتند، اصطلاح هایی كه هنوز هم معمول اند. در واقع توان دوم را به معنای مساحت و توان سوم را به معنای حجم می گرفتند و چون در زندگی عملی، با جسم چهار یا پنج بعدی سروكار نداریم، بحث درباره معادله های بالاتر از درجه سوم را - جز در حالت های نادر مثل معادله های سیال كرجی - بی معنی می دانستند.
فارابی در كتاب بزرگ موسیقی خود، برای نخستین بار در جهان، نظریه علمی موسیقی را مطرح می كند و جنبه های مختلف آن را مورد بحث قرار می دهد (در تقسیم بندی فارابی از دانش ها، موسیقی بخشی از ریاضیات به شمار می آید) پیش از فارابی، اگر از موسیقی عملی عیلام و بابل و مصر و هند بگذریم، تنها در یونان بحث هایی در زمینه موسیقی در جریان بود كه بیشتر جنبه متافیزیكی داشت و آمیخته با وهم و تخیل بود.
فارابی مبانی فیزیكی و ریاضی موسیقی را بررسی كرده و نخستین كتاب علمی موسیقی را ارائه داده است. ابوالوفا و بیرونی بیش از دیگران دستورهای مثلثاتی را كشف و ثابت كردند و این به دلیل دشواری هایی بود كه در اخترشناسی و محاسبه های مربوط به آن پیش می آمد. بطلمیوس بیشتر استدلال ها و محاسبه های خود را بر اساس هندسه و قضیه ها و مسئله های آن انجام می داد و این كار را بسیار دشوار می كرد. «ابوالوفای بوزجانی» و «ابوریحان بیرونی»، برای رفع این دشواری ها بود كه مثلثات را شكوفا كردند و پیش بردند و سرانجام «نصرالدین توسی» با تالیف «كشف القناع» خود استقلال مثلثات را از هندسه اعلام كرد. «جمشید كاشانی» برای همین محاسبه های اخترشناسی (او پایه گذار رصدخانه الغ بیگ در سمرقند بود) و به این دلیل كه راه های قبلی (مانند راه ابوالوفا)، اندكی طولانی و تا اندازه ای غیردقیق بود، روش جبری حل معادله درجه سوم: ۴x۳-۳x = a را برای پیدا كردن مقدار دقیق سینوس یك درجه (از روی سینوس سه درجه) به دست آورد.
ریاضیدانان ایرانی، اندازه سینوس زاویه های ،۱۵ ،۱۸ ،۳۰ ،۴۵ ،۶۰ ،۷۲ ۷۵ درجه (و در نتیجه، كسینوس آنها) را می شناختند و مقدار سینوس سه درجه را با بسط (۱۵- ۱۸) sin به دست می آوردند. باید به این نكته اشاره كنیم كه اغلب مورخان دانش حتی با انصاف ترین آنها نتوانسته اند مقام ریاضیات ایرانی را، در مجموعه تاریخ ریاضیات به درستی و روشنی ارزیابی كنند. اغلب آنها ریاضیدانان ایرانی را تا حد مترجمان ساده نوشته های یونانی پایین آورده اند كه این ترجمه ها هم به موقع خود، به صاحبان اصلی یعنی اروپاییان برگشت داده شده است. به این ترتیب مورخان ریاضی آغاز ریاضیات را در اروپا (یونان) می دانند كه بعد از سقوط مكتب اسكندریه در سده های سوم و چهارم میلادی، دوران فترتی به وجود می آید كه تا سده پانزدهم میلادی ادامه دارد و سپس با دسترسی اروپاییان به نوشته های یونانی (از راه ترجمه عربی آنها) دوباره دنبال كار را می گیرند و آن را به امروز می رسانند.
|
● مقدمه
اشکال هندسی در زندگی همیشه دارای کاربردهای فراوان بوده و برای فعالیتهای انسان الهام بخش و سمبل نیز شده است. دایره یکی از این اشکال است. ابتداییترین کاربرد دایره ، چرخ و چرخدندهها هستند که از قدیمالایام بکار رفته و میروند. همچنین ابزار آلات زینتی چون تاج ، گردبند ، خلخال و حلقهها ، کاربردی به اندازه تاریخ بشری دارند. نمونه مثال زدنی حلقه ازدواج است که بین زوجین مبادله میشود و این برگرفته از حلقهای است که در دست اهورامزدا در پیکرهها و مجسمهها دیده میشود.
با توجه به قرینه مذهبی قداست و پاکی ازدواج در ایران باستان را نشان میدهد که اکنون فرهنگی جهانی گشته است. دایره در فرهنگها ، انجمنها ، شهرسازی ، اندیشههای هنری و ریشهدار بخصوص در ابزار آلات نجومی جایگاه نمادین و کاربردی دارد. در فرهنگ و ادیان قدیم ازجمله بودا ، نماد آسمان ، جهان پاک ، افلاک گردنده و غیر دنیاست در حالی که در مقابل دنیا چهار گوشه و مربع است که به وضوح در بیان اشعار و ادبیات ایرانی بویژه غزلیات عرفانی مشاهده میشود.
● دایره در هنرهای اسلامی ایران
در هنرهای اسلامی ایرانی دایرهها ، به شکل شمس و حلقه نورانی در اطراف سرایمه و بزرگان دین دیده میشود. همچنین با توجه به کراهت صورتگری و مجسمه سازی در اسلام و ظریف اندیشی شیعه ، هنرهای اسلامی به شکلهای اسلیمی ، گل و بوته ، نقشهایی ختایی سوق داده شد. اشکال و خطوط و ترکیب رنگ در مینیاتورها ، تذهیبها و فرشها با زینت و ترکیب و نقش نگار پختهتری تکامل یافتند.
دایره به شکل شمسههای زیبایی تزیین داده شد و شمسهها به صورت منفرد یا در سایر هنرها کاربرد یافت. در خطوط گل و بوته و اشکال اسلیمی و ترکیب رنگ دایره به عنوان پایهایترین ، اصلیترین و اساسیترین شکل بکار گرفته میشود. و سیر کلی به سوی مرکز برای وصل فنا نقطهای (سیاه) است. که اختیار را از چشمان بیننده گرفته و با سیر در تابلو به مرکز هدایت میکند.
● دایره و نقطه سیاه و قرمز
در میان قبایل بدوی و بسیاری از انجمنها و دستههای سری قدیم ، سمبل مفاهیمی چون ابدیت ، جاودانگی و مرگ بوده است و دایره سیاره و دوایر متحدالمرکز در تمرینات اساسی ماینهتیستها ، هیپنوتیستها و درمانگران حرفهای میباشد. دایره و نقطه سرخ که اغلب نشان آفتاب میباشد در پرچم و سمبل ملل شرق آسیا نیز مشاهده میشود.
● هفت شهر
بطلیموس در دو قرن پیش از میلاد بر اساس تفاوت حرارت ، سرزمینهای شناخته شده آن روزگار را به هفت اقلیم تقسیم کرده است از آنجا که تقسیم بندی بطلیموس بر اساس دایرههای مداری است اقلیمهای هفت گانه را اقلیمهای هندسی نیز نامیدهاند. به نظر صاحبنظران ، اصطلاح هفت شهر ، هفت اقلیم و هفت وادی که در ادبیات و حکمت ایرانی وارد شده است الهامی از نظریات بطلیموسی را در خود دارد. اجرام آسمانی به دو دسته ثوابت و اجرام متحرک و متغیر تقسیم بندی شد و اجرام متغیر شناخته شده آن روز ، خورشید ، زمین ، بهرام ، تیر ، عطارد ، مشتری و زحل هر کدام در مداری و آسمانی تصور شدند. آسمان اول ، آسمان دوم … تا هفت آسمان.
● دایره و نجوم
کره زمین برای شناسایی بهتر به دایرههای افقی به نام مدار از صفر استوا تا ۹۰ درجه قطبین و دایرههای عمودی به نام نصفالنهار تقسیم بندی میشود. در علوم قدیم دایره بیشترین کاربرد و برترین جایگاه را در علم نجوم دارد. اولین مدلهای منظومهای بر اساس گردش زهره در فرهنگ اینکاها ، گردش خورشید و کاینات دور کلیسا و زمین ، تا گردش زمین و سیارات دور خورشید در نجوم اسلامی و قوانین حاکم بر حرکت آنها بر روی مسیرهای دایروی بودند. مدلهای اتمی بعد از نظریه جوزف تامسون نیز هسته متمرکز در مرکز (بار مثبت) و الکترونهای متحرک در مدارهای دایروی بود. که به دلیل شباهت به مدل منظومهای مشهور گشت.
بعدها تیکوبراهه ، کپلر ، کپرنیک روی این نظریهها کار کردند. در سال ۱۶۱۹ کپلر سه قانون حرکت سیارات را با استفاده از مشاهدات تیکوبراهه بیان کرد. قوانین کپلر پایه و اساس قوانین نیوتن و مکانیک کلاسیک و مکانیک سماوی شد. در این نظریه مسیر دایره به مسیر بیضوی که خورشید در یک کانون بیضی قرار دارد تغییر یافت. با مطرح شدن فیزیک نوین و فیزیک کوانتومی ، اصل عدم قطعیت و سایر پیشرفتهای تکنولوژیکی مدل منظومهای هسته نیز به مدل ابر الکترونی تبدیل گشت.
● نگاهی به رصدخانه مراغه
این رصدخانه در زمره پیشگامان نجوم ایران و دنیای قدیم بوده و جایگاه بینظیری برای خود دارد. مهمترین دوره و مکتب نجومی ایران مکتب مراغه بود که به گفته پروفسور عبدالسلام رصدخانههای هنر با وجود رگههای هنری اساسا بر پایه رصدخانههای اسلامی ساخته شده است. در این میان مکتب مراغه با نام خواجه نصیرالدین طوسی با سمت گیری انتقادی نسبت به نظام بطلیموسی به دلیل مشکلات جدی و ناسازگاریهای ذاتی موجود اخترشناسان بر اساس مدل هندسی نجومی ارایه شد که به جفت طوسی معروف گشت. ایجاد حرکت خطی به کمک حرکتهای دورانی یکنواخت است. ساختمان اصلی این رصدخانه به شکل استوانه طراحی شده بود. اکثر وسیلههای رصدی در آن شکل دایروی داشتند از مهمترین وسیلههای رصدخانه مراغه میتوان به موارد زیر اشاره کرد.
● وسایل رصد خانه مراغه
سدس فخری که بعدها با اصلاح به دوربینهای تیودولیت معروف گشتند که کاربردهای نقشه برداری دارد. وسیله دیگر ربع بود. این آلت از ربع دایره و عضادهای تشکیل یافته و با آن میل کلی و ابعاد کواکب و عرض بلد را رصد مینمودند و بر سطح دیواره شمالی و جنوبی رصدخانه نصب شده بود. وسیله دیگر ذاتالحلق بود که که به جای ششگانه بطلیموس و نه حلقه ثاون اسکندرانی جامعتر بوده است.
آلتی است متشکل از پنج حلقه به ترتیب الف برای دایره نصف النهار که بر زمین نصب شده بود. ب برای دایره معدل النهار ج برای دایره منطقهالبروج د برای دایره عرض و ه برای دایره میل. از آلات دیگر رصدخانه مراغه ذاتالجیب و ذاتالسمت بودند که برای تعیین ارتفاع در کلیه جهات مختلف افق بکار رفته میشد. ذاتالربعین که به جای ذاتالحلق استعمال میشد. ذاتالارسطوانتین و دایره شمسیه از وسایل دیگر رصد خانه هستند.
نگاهی به استفاده از دایره برای رفع مشکلات شهرها و شهرسازی
توسعه شهرها ، تامین نیازمندیهای آنان ، چارهجویی برای توسعههای آینده شهر ، اتخاذ تصمیماتی که بتواند مشکلات شهری را به حداقل برساند و بالاخره آنکه چگونه رابطه منطقی بین انسان با محیط طبیعتش حفظ شود، به تحولاتی در امر شهرسازی منجر شد. نخستین نظریه در زمینه شهرسازی شخصی به نام هیپوداموس (۴۸۰ سال قبل از میلاد) بود و بعد از آن نظریات و راهکارهای متفاوت شهرسازی بوجود آمد. ولی پیدایش دانش امروزی شهرسازی به قرن نوزده میلادی میرسد. از میان نظریههای شهرسازی میتوان نظریههای زیر را نام برد.
● نظریه متحدالمرکز
در این نظریه الگوی ساخت شهر بر این اصل استوار است که توسعه شهر از ناحیه مرکزی به طرف خارج شهر صورت گرفته و تعداد مناطق متحدالمرکز را تشکیل میدهد. این مناطق با ناحیه مشاغل مرکزی شروع شده و بوسیله منطقه در حال تحول احاطه میشود.
● نظریه قطاعی
تعدیل و تغییر در جهات مختلف این نظریه است. شهرها برای همیشه نمیتوانند حالت متحدالمرکزی مناطق را حفظ کنند. در این نظریه اجازه خانه به عنوان راهنما مطالعه شهر را عملی میسازد. ساخت واحدهای گرانقیمت از کانون اصلی در طول شبکههای رفت و آمد ، ساخت واحدهای مسکونی دیگر و ارزانتر به سوی فضاهای باز و جابجایی ساختمانهای اداری و تجاری ، توسعه واحدهای مسکونی گرانقیمت را در جهت عمومی عملی سازد. آپارتمانهای لوکس در مجاورت بخشهای تجاری و مسکونی قدیمی بوجود آمده و واحدهای گرانقیمت شهر بطور اتفاقی و نامنظم جابجا نمیشوند. راههای شعاعی از مرکز شهر به اطراف کشیده میشود و عامل دسترسی به این راهها و قیمت زمینها را در مناطق مختلف شهر تعیین میکند.
● مدل حلقهای
در این مدل به جای آنکه خطوط اصلی حمل و نقل به صورت خطی گسترش یابد به شکل دایرهای و به موازات مرکز شهر ، حواشی ناحیه مرکزی و بافتهای اطراف آن را احاطه میکند. و دور تا دور بافت را گرههای شهری بوجود میآورد. و فعالیتها شکل حلقهای یا زنجیرهای به خود میگیرند.
● طرح مکمل مدل کهکشان
بر اساس نظریه ویکتورگروین در بیشتر شهرهای بزرگ کاربرد دارد. شهر از مراکز متعددی تشکیل یافته و هر کدام واحدهای دیگری را بوجود میآورد و بوسیله شبکههای ارتباطی مشترک و مستقل و منطقهای بافتها به همدیگر مرتبط میشوند. مجموعه این بافتها و شبکهها یک شبکه کهکشانی را بوجود میآورد. خدمات مرکزی در وسط بافت و جایگاه صنایع در نواحی اطراف شهر و در خارج از بافت اصلی پیشبینی شده است.
● دایره در مثلثات و فیزیک
از دایرههای مشهور دیگر دایره مثلثاتی است. دایره مثلثاتی دایرهای است با درجهبندی و جهت حرکت مشخص که به آن جهت مثلثاتی گویند و آن پادساعت گرد یا عکس ساعت گرد است. شعاع این دایره واحد است و حداکثر مقدار توابع مثلثاتی سینوس یا کوسینوس که در این دایره بدست میآید میتواند واحد شود. هارمونیها و هماهنگها ، چرخش ، حرکت دورانی ، حرکات پریودیک و دورهای ، حرکات تناوبی ، حرکات رفت و برگشتی در یک مسیر مشخص را میتوان توسط این دایره و کمیات مثلثاتی برای بیان مکان و زمان و توصیف این حرکات و موقعیت بکار برد.
دایره در ورزشهای باستانی و موسیقی
دایره با توجه به نماد آسمانی و قداست افلاکی در ورزشهای باستانی از جمله زورخانه و گوی بازی ورزشکاران باستانی کار ، در رقص سماء و حلقه گردش و لباس و کلاه آنها ، نیز کاربرد دارد. در مکاتب هادی همچون کومونیسم نیز همچنان که در فیلم بایکوت مشاهده میکنیم. به عنوان سمبل بکار رفته است مسیری که از هیچ آغاز شده و در سیر مسیر به هیچ منتهی میشود.
اساس موسیقی و هنرهای ادبی شرقی موسیقی دوری است. موسیقی و هنری که انسان را در جای خود از حالی به حالی دگرگون میکند از نقطهای شروع شده و او را به سیر در عالم معانی برده و در آخر انسانی ارزشی ، تحول یافته و والامقام و انسانی که شایسته خلیفه الهی است بوجود میآورد.
|
یکی از معمول ترین سوالهایی که مطرح می شود این است که: چه کسی صفر را کشف کرد؟ البته برای جواب دادن به این سوال بهدنبال این نیستیم که بگوییم شخص خاصی صفر را ابداع و دیگران از آن زمان به بعد از آن استفاده می کردند.
اولین نکته شایان ذکر در مورد عدد صفر این است که این عدد دو کاربرد دارد که هر دو بسیار مهم تلقی می شود یکی از کاربردهای عدد صفر این است که به عنوان نشانه ای برای جای خالی در دستگاه اعداد (جدول ارزش مکانی اعداد) بکار می رود. بنابراین در عددی مانند ۲۱۰۶ عدد صفر استفاده شده تا جایگاه اعداد در جدول مشخص شود که بطور قطع این عدد با عدد ۲۱۶ کاملاً متفاوت است. دومین کاربرد صفر این است که خودش به عنوان عدد بهکار می رود که ما به شکل عدد صفر از آن استفاده می کنیم.
هیچکدام از این کاربردها تاریخچه پیدایش واضحی ندارند. در دوره اولیه تاریخ کاربرد اعداد بیشتر بطور واقعی بوده تا عصر حاضر که اعداد مفهوم انتزاعی دارند. بطور مثال مردم دوران باستان اعداد را برای شمارش تعداد اسبان، … بکار می برند و در اینگونه مسایل هیچگاه به مسیله ای برخورد نمی کردند که جواب آن صفر یا اعداد منفی باشد.
بابلیها تا مدتها در جدول ارزش مکانی هیچ نمادی را برای جای خالی در جدول بکار نمی بردند. می توان گفت از اولین نمادی که آنها برای نشان دادن جای خالی استفاده کردن گیومه (”) بود. مثلاً عدد۶″۲۱ نمایش دهنده ۲۱۰۶ بود. البته باید در نظر داشت که از علایم دیگری نیز برای نشان دادن جای خالی استفاده می شد ولیکن هیچگاه این علایم به عنوان آخرین رقم آورده نمی شدندبلکه همیشه بین دو عدد قرار می گیرند بطور مثال عدد “۲۱۶ را با این نحوه علامت گذاری نداریم. به این ترتیب به این مطلب پی می بریم که کاربرد اولیه عدد صفر برای نشان دادن جای خالی اصلاً به عنوان یک عدد نبوده است.
البته یونانیان هم خود را از اولین کسانی می دانند کهدرجای خالی ,صفر استفاده می کردند اما یونانیان دستگاه اعداد (جدول ارزش مکانی اعداد) مثل بابلیان نداشتند. اساساً دستاوردهای یونانیان در زمینه ریاضی بر مبنای هندسه بوده و به عبارت دیگر نیازی نبوده است که ریاضی دانان یونانی از اعداد نام ببرند زیر آنها اعداد را بعنوان طول خط مورد استفاده قرار می دادند.
البتهبعضی ازریاضی دانان یونانی ثبت اطلاعات نجومی را بر عهده داشتند. در این قسمت به اولین کاربرد علامتی اشاره می کنیم که امروزه آن را به این دلیل که ستاره شناسان یونانی برای اولین بار علامت ۰ را برای آن اتخاذ کردند، عدد صفر می نامیم. تعداد معدودی از ستاره شناسان این علامت را بکار بردند و قبل از اینکه سرانجام عدد صفر جای خود را بدست آورد، دیگر مورد استفاده قرار نگرفت و سپس در ریاضیات هند ظاهر شد.
هندیان کسانی بودند که پیشرفت چشمگیری در اعداد و جدول ارزش مکانی اعداد ایجاد کردند هندیان نیز از صفر برای نشان دادن جای خالی در جدول استفاده می کردند.
اکنون اولین حضور صفر را به عنوان یک عدد مورد بررسی قرار می دهیم اولین نکته ای که می توان به آن اشاره کرد این است که صفر به هیچ وجه نشان دهنده یک عدد بطور معمول نمی باشد. از زمانهای پیش اعداد به مجموعه ای از اشیاء نسبت داده می شدند و در حقیقت با گذشت زمان مفهوم صفر و اعداد منفی که از ویژگیهای مجموعه اشیاء نتیجه نمی شدند، ممکن شد. هنگامیکه فردی تلاش می کند تا صفر و اعداد منفی را بعنوان عدد در نظر بگیرید با این مشکل مواجه می شود که این عدد چگونه در عملیات محاسباتی جمع، تفریق، ضرب و تقسیم عمل می کند. ریاضی دانان هندی سعی بر آن داشتند تا به این سوالها پاسخ دهندو در این زمینه نیز تا حدودی موفق بوده اند .
این نکته نیز قابل ذکر است که تمدن مایاها که در آمریکای مرکزی زندگی می کردند نیز از دستگاه اعداد استفاده می کردند و برای نشان دادن جای خالی صفر را بکار می برند.بعدها نظریات ریاضی دانان هندی علاوه بر غرب، به ریاضی دانان اسلامی و عربی نیز انتقال یافت. فیبوناچی، مهمترین رابط بین دستگاه اعداد هندی و عربی و ریاضیات اروپا می باشد.
|
|
|
|
معرفی اجمالی انواع طراحی سیستم های سازه ای









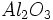 و
و 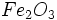 ). به دلیل رطوبت ، سدیم ، کلسیم ، منیزیم و پتاسیم در آب زیرزمینی حل و برای ریشههای گیاهان غیر قابل دسترس میشوند. به دلیل آزاد بودن یون هیدروژن ، خاکهای لاتریتی بسیار اسیدی هستند.
). به دلیل رطوبت ، سدیم ، کلسیم ، منیزیم و پتاسیم در آب زیرزمینی حل و برای ریشههای گیاهان غیر قابل دسترس میشوند. به دلیل آزاد بودن یون هیدروژن ، خاکهای لاتریتی بسیار اسیدی هستند. 







